O uso da abordagem multinível para previsão de falhas em aerogeradores

_{DOI: 10.22167/2675-6528-20230110}
^{E&S 2023,4: e20230110}

João Gilberto Máximo Da Silva; José Erasmo Silva

A indisponibilidade de um aerogerador causada por uma falha inesperada de um componente, além dos custos com a manutenção associada à dificuldade de acesso de alguns parques eólicos, gera instabilidade na geração de energia, podendo impactar não somente as empresas que operam os parques eólicos, mas também milhares de pessoas que dependem da energia gerada nestes parques.

Em um mercado global cada dia mais competitivo, as empresas buscam a otimização de seus processos de modo a serem cada vez mais produtivas. Dentro deste contexto, a disponibilidade dos ativos industriais se torna um item muito importante para a garantia da produtividade, e a área de manutenção impacta diretamente estes resultados operacionais^[1].

Dentre os diversos métodos de manutenção aplicados hoje, a manutenção preditiva se destaca pela capacidade de diagnosticar possíveis falhas de equipamentos em seu estágio inicial, evitando assim quebras inesperadas. Um bom planejamento com o uso das técnicas de manutenção preditiva, contribuem para o aumento da vida útil dos ativos, diminuindo os custos^[2].

Um dos métodos de manutenção preditiva mais poderosos e que ainda é amplamente utilizado é a inspeção visual^[3]. Esse método tem evoluído para a utilização de modelos automatizados que fazem a coleta, o tratamento e a previsão de eventos utilizando “machine learning”.

O avanço nas pesquisas e as publicações voltadas à manutenção preditiva por análise de vibrações, têm se mostrado relevantes nos últimos anos. Podemos atribuir a este cenário o crescente número de dados obtidos através de sistemas cada vez mais integrados entre si, e o avanço na difusão e utilização de algoritmos de “machine learning” como ferramentas para tratar e entender o volume enorme de informações obtidas destes sistemas^[4].

Embora os modelos de regressão logística sejam muito úteis e fáceis de implementar, ainda são pouco aplicados em muitas áreas do conhecimento humano. Diferentemente da técnica tradicional de regressão estimada pelo método de mínimos quadrados, em que a variável dependente é apresentada quantitativamente, o fenômeno a ser estudado é apresentado qualitativamente e, portanto, figurado por uma variável indicadora, podendo ter duas ou mais categorias^[5].

Contudo, vale ressaltar que, em geral, os modelos tradicionais de regressão não conseguem capturar as interações entre os componentes de efeitos fixos e as interações entre as variáveis nos componentes de efeitos aleatórios e os termos de erro. Nesse contexto, a abordagem multinível surge como uma alternativa promissora. Ela apresenta vantagem para este estudo deste caso, pois leva em consideração a análise dos dados hierarquicamente estruturados^[6]. O conceito de análise de vibrações, no qual a manutenção preditiva está inserida, aborda cada equipamento industrial como uma parte de um conjunto. Este, por sua vez, constitui um parque de máquinas. Assim, a natureza hierárquica dos dados justifica a escolha desta técnica para o estudo em questão.

Com base no que foi discutido, o presente estudo tem como objetivo empregar a modelagem multinível logística na construção de um modelo preditivo. Esse modelo visa identificar a necessidade de manutenção em aerogeradores utilizando dados vibracionais como referência. Para alcançar esse propósito, informações relacionadas aos parâmetros de vibração gerados por esses equipamentos serão coletadas e meticulosamente analisadas.

O estudo utilizou um conjunto de dados contendo registros históricos de análises vibracionais em aerogeradores, coletados entre 2010 e 2012. Estes dados foram obtidos de uma fonte industrial confidencial, garantindo a privacidade e a não divulgação da empresa em questão. Cada aerogerador, situado em uma região única, apresenta uma organização hierárquica distinta no conjunto de dados, destacando a natureza multinível das informações. A base de dados engloba 117 torres eólicas, agrupadas em parques com no máximo 11 torres cada, distribuídas por três continentes: Ásia, Europa e América do Norte. Apesar da abrangência em número de torres, uma das limitações do estudo foi tratar as mais de 48 milhões de linhas de dados gerados a partir das torres. Nesse sentido, optou-se por transformar os dados originais gerados de 10 em 10 minutos para a média diária desses dados.

A técnica de análise de vibrações conta com uma gama enorme de tecnologias desenvolvidas para aprimorar a coleta e a análise dos dados vibracionais oriundos dos equipamentos rotativos^[7],[8]. Para o estudo, utilizaram-se os dados provenientes de uma destas tecnologias disponíveis no mercado. Trata-se se um módulo de aquisição que realiza a função de coletor e analisador de vibrações; uma vez configurado para sua finalidade, esse módulo realiza a coleta de dados de vibração em tempo real, sem a necessidade de intervenção humana. Através de configurações realizadas via software proprietário, o módulo realiza as medições e as disponibiliza diretamente no software, onde um analista de vibrações realiza as análises e diagnostica o status do aerogerador, classificando em níveis de criticidade baseados na norma ISO 20816-3. Para cada torre presente no banco de dados, parâmetros de monitoramento condicional dos componentes do aerogerador foram coletados em pontos pré-definidos e em comum para todas as torres. A Figura 1 ilustra a disposição dos pontos de medição.

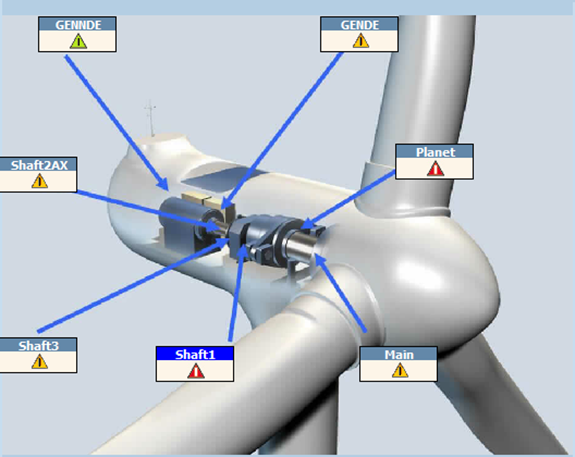
Figura 1. Pontos de medição de vibração nos componentes do aerogerador
Fonte: Dados originais do trabalho.

Em cada ponto de medição foi disposto um sensor de aceleração do tipo piezelétrico, cada sensor por sua vez realiza o registro dos parâmetros vibracionais do componente em que foi instalado, desta forma é possível obter os valores globais de vibração para cada grandeza medida.

Os pontos de medição são determinados por meio dos mancais de eixo mais importantes de todo o equipamento. Um acionamento de um aerogerador é definido por^[9]:

• eixo principal “Main”: é o eixo acoplado as hélices do aerogerador, o vento impulsiona as hélices que por sua vez giram o eixo principal;
• engrenagem de entrada do planetário (Planet): a rotação do eixo principal é amplificada graças a um conjunto de engrenagens que aumentam a relação de transmissão, de modo que a velocidade de rotação do eixo de saída (Shaft3), seja maior que a velocidade de rotação do eixo de entrada “Main”;
• eixo intermediário “Shaft2AX”: trata-se do eixo intermediário do conjunto de engrenagens, composto por pinhão e coroa dentadas, o acrônimo AX é usado para indicar que o posicionamento do sensor é axial em relação ao eixo.
• eixo de saída “Shaft3”. é o eixo de saída do sistema amplificador de velocidade. Este ponto é acoplado diretamente no gerador, onde a energia é gerada;
• mancal acoplado do gerador “GEN_DE”. é o mancal frontal do gerador, onde existe o acoplamento com o eixo de saída do sistema de amplificação de velocidade;
• mancal oposto ao acoplado do gerador “GEN NDE”. trata-se do mancal traseiro do gerador, faz parte do eixo do gerador, onde o rotor, responsável pela geração de energia, está instalado.

Os parâmetros medidos em diferentes pontos são divididos entre operacionais (que se referem à operação do aerogerador, com “Puissance”, ou potência gerada) e vibracionais (que se referem ao valor de vibração gerado pelo aerogerador no instante da coleta, como “Ng Accélération” ou Nível Global de Aceleração). Dentre os principais parâmetros avaliados, priorizou-se definir aqui aqueles que foram estatisticamente significantes após o procedimento “stepwise” para o modelo logístico binário^[5], e que foram descritos abaixo:

• “Puissance” (Potência): parâmetro operacional, obtido por meio do sistema “Supervisory Control And Data Acquisition” [SCADA], que informa a potência gerada em MW/h no momento da aquisição;
• “VitesseRotation” (Velocidade de Rotação): velocidade angular do eixo principal;
• “VitesseVent” (Velocidade do Vento): parâmetro operacional, obtido por meio do sistema SCADA, que informa a velocidade do vento em m/s no momento da aquisição. Para o estudo, foram consideradas as maiores velocidades filtradas do sistema de aquisição, no intuito de observarmos o cenário de maior efeito vibratório;
• “OVL_ACC” (Aceleração Global): o nível global de vibração é um número obtido a partir de um cálculo que considera as diversas frequências e suas respectivas amplitudes presentes no espectro, neste caso no espectro de aceleração;
• “OVL_VEL” (Velocidade de Vibração Global): o nível global de vibração é um número obtido a partir de um cálculo que considera as diversas frequências e suas respectivas amplitudes presentes no espectro, neste caso o espectro de Velocidade de Vibração. Todos estes parâmetros são utilizados por analistas de vibração para identificar possíveis falhas nos componentes de máquinas rotativas em geral.

Os dados referentes às medições realizadas em cada ponto foram exportados do banco de dados original em formato .CSV e, posteriormente, carregados no software R e IDE RStudio para tratamento e análise^[10],[11].

Aplicando-se a técnica supervisionada de “machine learning” conhecida como Logística Binária, o objetivo foi explicar a probabilidade de ocorrência do evento estudado, neste caso, a probabilidade de um componente do aerogerador entrar em alarme, em função das variáveis explicativas, que, para este estudo, são representadas pelos valores de vibração associados aos parâmetros de monitoramento. Portanto, foi aplicado o método de Máxima Verossimilhança para estimar os parâmetros da função logística; em seguida, foi verificada a significância estatística dos parâmetros estimados pelo método^[5].

Em sequência, utilizou-se a modelagem multinível para capturar os comportamentos de grupo, bem como os efeitos aleatórios decorrentes de uma estrutura multinível. Na modelagem multinível, além da natureza dos dados, é importante a observação da estrutura do “dataset” e da disposição dos dados, de modo que seja possível observar níveis contextuais. A análise multinível permite então, a elaboração de novos construtos, não observáveis no modelo logístico.

Para as duas situações, as métricas de maior interesse para avaliação dos modelos foram a curva ROC, a sensitividade e a especificidade. A sensitividade refere-se à porcentagem de acertos para um determinado critério, considerando apenas as observações evento, ou seja, os valores preditos como eventos e que realmente o são. A especificidade refere-se à porcentagem de acertos para um determinado critério, considerando apenas observações não evento. Já a curva ROC mostra o comportamento real do equilíbrio entre sensibilidade e especificidade. Nesse sentido, um determinado modelo com uma grande área sob a curva ROC proporciona uma maior eficiência preditiva global^[5].

Após o processo de Extração, Tratamento e Carga, os dados foram submetidos à modelagem logística no software R,  foi possível extrair as informações que conduziram este estudo. Para a análise logística binária considerou-se como variável resposta o STATUS de alarme de cada parâmetro observado, o qual indica os níveis de alarme definidos no sistema de aquisição e que auxiliam o analista de vibrações na tomada de decisão. A Tabela 1 apresenta os tipos de STATUS oriundos do banco de dados.

Tabela 1. STATUS dos parâmetros

STATUS	SIGNIFICADO
DNG	PERIGO – Alarme de nível 2
ALM	ALARME – Alarme de nível 1
PRE	PRÉ-ALARME – Status antes do alarme de nível 1
RAS	Ausência de alarmes

Como para o analista de vibração o STATUS de alarme de nível 2 é o mais crítico, nesta etapa o STATUS “DNG” foi classificado como ocorrência do evento, portanto é possível com valor 1 (um), e os demais STATUS foram classificados como não evento ou valor 0 (zero). Como é possível observar na Tabela 2, após a transformação dos STATUS em valores binários, foram obtidas as métricas referentes à quantidade de eventos e não eventos da variável resposta.

Tabela 2. Variável resposta após processo de “Dummy”                       

Fracasso 0 (zero)	Sucesso “DNG” 1 (um)
16325 (86,6%)	2525 (13,4%)

Na Tabela 3 é possível observar as estatísticas descritivas das variáveis explicativas de maior relevância dentro do “dataset”.

Tabela 3. Estatísticas descritivas dos parâmetros de vibração

Variável	Min	1° Quartil	Mediana	Média	3° Quartil	Max
Puissance	-0,1012	0,363	0,43	0,536	0,675	1,195
VitesseVent	0,00875	7,064	7,57	7,785	8,384	36,174
VitessRotat	0,4619	21,618	22,84	24,013	26,062	30,274
OVL_ACC	0,00660	0,2724	0,3625	0,41392	0,4810	2,2927
OVL_VEL	0,01207	0,539	0,696	0,8928	1,057	25,6592

 Em sequência, foi aplicado o procedimento de “stepwise” de modo a capturar as maiores relevâncias estatísticas das variáveis explicativas, excluindo aquelas que não têm grande relevância para o modelo, ou seja, não apresentam significância estatística suficiente para explicar o evento^[5]. Por meio da Tabela 4, pode-se observar que a Puissance (Potência) tem um impacto negativo na probabilidade de falha. Nesse sentido é possível afirmar que os equipamentos mais potentes estão menos sujeitos a falhas na amostra estudada. Nota-se ainda que a Vitesse_Rotation (Velocidade de Rotação) tem um impacto positivo, ou seja, quanto maior a velocidade, mais sujeito a falhas estará o equipamento. Desta forma, outros estudos podem ser realizados com o objetivo de definir a velocidade ideal para que o equipamento continue produtivo, mas menos sujeito a falhas. Por fim, as variáveis OVL_ACC (Aceleração Global) e OVL_VEL (Velocidade de Vibração Global) também apresentaram coeficientes positivos, indicando maior probabilidade de falhas com o aumento desses fatores.

Tabela 4. Coeficientes estimados após “stepwise”                                                                     

Variáveis	Estimado	Err Padrão	Zvalor	Pr (>|z|)	Sig.
(Intercepto)	-11,115	1,27854	-8,693	2,00E-16	***
Puissance	-8,48461	0,99015	-8,569	2,00E-16	***
Vitesse_Rotation	0,48235	0,07591	6,354	2,1e-10	***
OVL_ACC	2,92158	0,10763	27,145	2,00E-16	***
OVL_VEL	0,8029	0,05008	19,574	2,00E-16	***

Contudo, ao analisar a matriz de confusão, responsável por indicar os acertos e erros do modelo de classificação, confrontando os eventos reais com os eventos preditos pelo modelo, observou-se que este apresenta um índice de acerto baixo em relação aos eventos preditos como TRUE e que realmente apresentam valor TRUE, para um “cutoff” padrão de 50%.

Tabela 5. Matriz de confusão

		REAL
		VERDADEIRO	FALSO	TOTAL
PREVISTO	VERDADEIRO	233	187	420
	FALSO	2292	15429	17721
	TOTAL	2525	15616	18141

Apesar de uma acurácia interessante na casa dos 86%, o modelo apresentou sensitividade baixa e uma especificidade alta, 9,2% e 98,8%, respectivamente, conforme visto na Tabela 6.

A área abaixo da curva ROC é um índice importante para avaliação global do modelo, pois mostra graficamente a relação entre especificidade e sensitividade para diferentes valores “cutoff”; dentro deste contexto, o modelo apresentou uma área abaixo da curva ROC de 73,9%, conforme é possível observar na Figura 2.

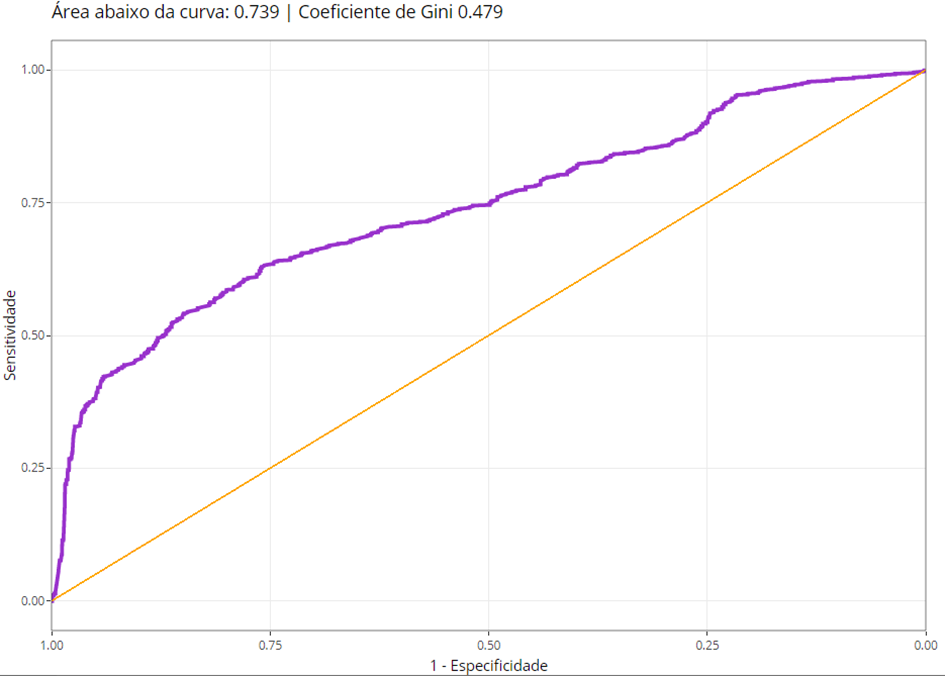
Figura 2. Curva ROC
Fonte: Resultados originais da pesquisa.

Após a análise dos resultados obtidos pelo modelo logístico binário, empregou-se a metodologia multinível para identificar os efeitos aleatórios associados a diferentes grupos. Levando em consideração que as torres estão distribuídas em diversas regiões do globo, os grupos foram separados no “dataset”. Estas torres foram categorizadas por “farms”, termo utilizado para designar os parques eólicos. Vale ressaltar que uma única região pode abrigar múltiplas “farms”.

A pesquisa analisou um total de 117 torres eólicas. Estas torres estão distribuídas em parques que contêm até 11 torres cada e estão localizadas em três continentes distintos: Ásia, Europa e América do Norte. Vale destacar que uma única região geográfica pode abrigar várias “farms”. Por exemplo, a Europa, tem-se as “farms” WF1, WF2_L1 e WF2_L2, como ilustrado na Figura 3.

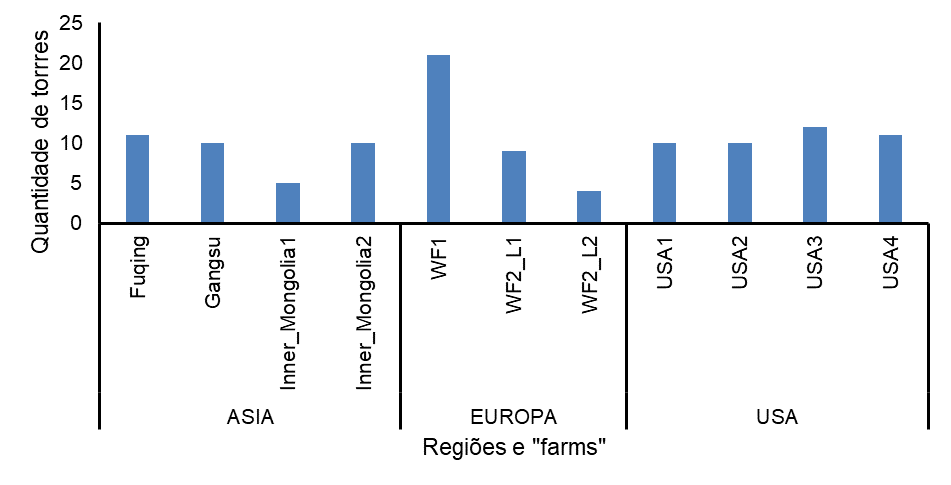
Figura 3. Número de torres por “farms” e região
Fonte: Resultados originais da pesquisa

Sendo os modelos hierárquicos multinível capazes de capturar a decomposição da variância dos efeitos aleatórios de grupo, onde a variável resposta se apresenta de forma categórica, como observado até então, o princípio foi justamente dicotomizar a variável STATUS, de maneira análoga ao que havia sido realizado na análise com a metodologia logística binária[5]. Porém, desta vez, além de considerar como evento a categoria “DNG” (Perigo), incluiu-se a categoria “ALM” (Alarme) também como evento. A Tabela 7, mostra como ficaram as contagens dos não eventos x eventos após a dicotomização da variável STATUS. Nota-se que, em relação ao primeiro modelo, o acréscimo no número de eventos foi de aproximadamente 265%, resultando assim em 63,10% de não eventos e 36,9% de eventos.

Tabela 7. Varável resposta após processo de “Dummy”                                                  

Fracasso 0 (zero)	Sucesso “DNG” e “ALM” 1 (um)
11447 (63,10%)	6694 (36,9%)

Ainda na transformação do “dataset”, incluiu-se a derivação da variável DATA DE MEDIÇÂO em “dummies”, com o objetivo de observar a influência de efeitos climáticos (estações do ano) na variável resposta.  Deste modo os meses foram dispostos como categorias para a criação das “dummies”. Após este procedimento, foi gerado o modelo multinível que apresentou os seguintes parâmetros após estimado, conforme Tabela 8.

Tabela 8. Resultados do modelo multinível com interceptos aleatórios

Variáveis	Estimado	Erro Padrão	z valor	Pr(>|z|)	Sig.
(Intercepto)	-2,15826	0,66310	-3,25	0,00113	**
Puissance	-3,63266	0,13518	-26,87	< 2e-16	***
OVL_ACC	7,00496	0,15169	46,18	< 2e-16	***
OVL_VEL	1,81259	0,05710	31,74	< 2e-16	***
Arret_Acceleration	-0,71068	0,04476	-15,88	< 2e-16	***
mes_2	0,73728	0,06296	11,71	< 2e-16	***
mes_3	0,18792	0,06620	2,84	0,00453	**
mes_4	0,29344	0,06575	4,46	8,08e-06	***
mes_5	-0,18472	0,06084	-3,04	0,00240	**
mes_7	0,17836	0,05842	3,05	0,00227	**
mes_8	0,16693	0,05680	2,94	0,00330	**
mes_9	-1,15504	0,12609	-9,16	< 2e-16	***
mes_10	0,23240	0,11799	1,97	0,04889	*
mes_11	-2,16955	0,12854	-16,88	< 2e-16	***
mes_12	-0,68953	0,10325	-6,68	2,41e-11	***

A partir da Tabela 8 é possível perceber que os sinais dos coeficientes se mantiveram compatíveis com a regressão logística sem multinível, no entanto, com valores diferentes. Os valores diferentes se deram em função de outras variáveis que foram inseridas nos efeitos fixos, especialmente os meses, bem como em função dos níveis aleatórios região e “farm”. Como os meses foram inseridos como “dummies”, os seus resultados se dão em comparação ao mês de janeiro (mes_1) que foi inserida como variável de referência. Desta forma, pode-se interpretar que o mês de novembro (mês_11) tem probabilidade menor de falha em relação a janeiro; por outro lado o mês de fevereiro tem uma probabilidade maior em relação a janeiro. Também se estimaram os parâmetros dos efeitos aleatórios, conforme apresenta a Tabela 9.

Tabela 9. Estatísticas dos efeitos

Nomes dos Grupos		Variância	Desvio Padrão
região	(Intercepto)	0,04424	0,2103
farm	(Intercepto)	4,32420	2,0795

A Tabela 9 mostra que a variância maior ocorre entre as diferentes fazendas (“farm”) e que a variância entre as regiões é discreta.  Para avaliar a matriz de confusão, foi elaborado um gráfico no software R, visando identificar o ponto ótimo de interseção entre os valores de sensitividade e especificidade. Conforme ilustrado na Figura 4, o ponto de corte (“cutoff”) selecionado para a construção da matriz de confusão foi estabelecido em 30%.

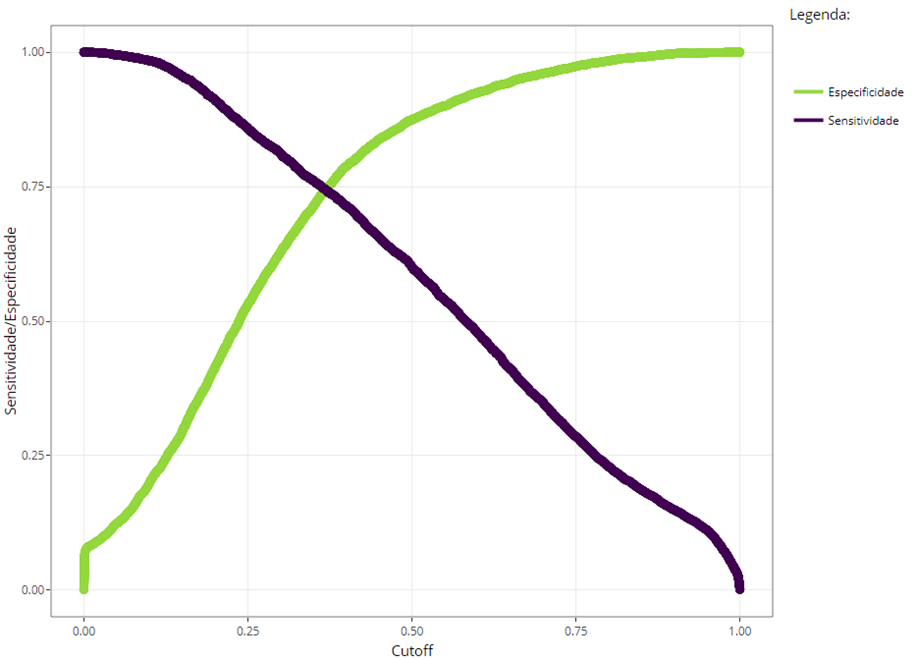
Figura 4. Gráfico sensitividade x especificidade
Fonte: Resultados originais da pesquisa

Com o melhor “cutoff” definido, pôde-se então gerar a matriz de confusão e os parâmetros para avaliação do modelo, como os valores de sensitividade, ou seja, o quão acurado é o modelo ao classificar os eventos, e a especificidade, ou seja, o quão acurado é o modelo em evitar falsos positivos. Ressalta-se o acréscimo considerável da sensitividade em relação ao modelo logístico binário (cerca de 71,8% de acréscimo), enquanto a especificidade teve uma pequena retraída. A Tabela 10 mostra a matriz de confusão e os parâmetros de avaliação.

Tabela 10. Matriz de confusão

		REAL
		VERDADEIRO	FALSO	TOTAL
PREVISTO	VERDADEIRO	6799	4922	11721
	FALSO	1585	8317	9902
	TOTAL	8384	13239	21623

Tabela 11. Parâmetros de avaliação

Métrica	Valor
Acurácia	0,6991
Sensitividade	0,8109
Especificidade	0,6282
Acurácia balanceada	0,7196

Ao analisar a Tabela 11 em comparação com a Tabela 6, é evidente que algumas métricas apresentaram piora, enquanto outras demonstraram melhorias. Essa mudança se deve ao ponto em que o corte foi aplicado. No caso do modelo logístico multinível, optou-se por um corte de 30%, em contraste com o modelo logístico binário, no qual foi utilizado o corte padrão de 50%. No entanto, é crucial destacar que o objetivo de ajustar o valor de “cutoff” foi alcançado, ou seja, conseguiu-se equilibrar os valores das métricas, mas vale ressaltar que o ponto ideal de “cutoff” pode variar dependendo do fenômeno em estudo.

Além das métricas avaliadas acima, outra métrica importante é a área sob a curva ROC, pois ela desempenha um papel crucial na avaliação abrangente do modelo. Nesse contexto, é notável que o modelo logístico multinível tenha alcançado uma área sob a curva ROC de 81,9%, representando um aumento de 8% em comparação com o modelo logístico binário, conforme ilustrado na Figura 5.

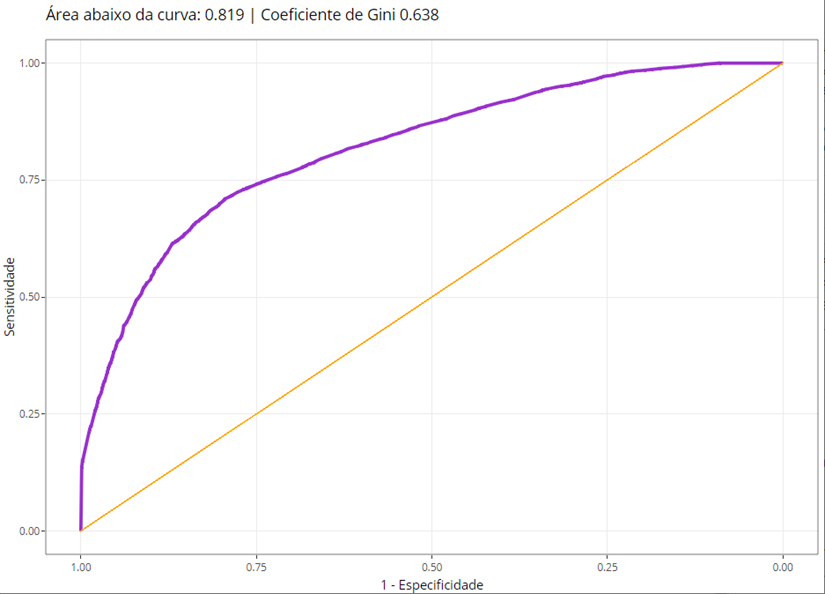
Figura 5. Curva ROC
Fonte: Resultados originais da pesquisa

O estudo teve sucesso no alcance do objetivo principal ao demonstrar as respectivas curvas ROC dos modelos logístico binário e multinível logístico, de modo que foi possível observar que este último apresenta maior eficiência preditiva global; deste modo, a aplicação de modelagem multinível, levando em consideração a influência de efeitos aleatórios impossíveis de se capturar com a modelagem logística binária, mostra-se uma técnica relevante para a predição de falhas em aerogeradores.

Referências

[1] Brito J. N. 2017. Plano De Manutenção de Ativos Físicos Como Parte Estratégica do Negócio. In: XVII Congresso Nacional de engenharia mecânica e industrial, 2017, Joinville, SC, Brasil. Disponível em: <http://doi.org/10.17648/conemi-2018-91231>. Acesso em: 16 out. 2022.

[2] Brito J. N. Marques A. C. 2019. Importância da manutenção preditiva para diminuir o custo em manutenção e aumentar a vida útil dos equipamentos. Brazilian Journal of Development. 5(7): 8913-8923. Disponível em: <https://doi.org/10.34117/bjdv5n7-095>. Acesso em: 16 out. 2022

[3] Hashemian H. M. 2011. State-of-the-Art Predictive Maintenance Techniques. IEEE Transactions on Instrumentation and Measurement. 60(1): 226–236. Disponível em: < https://doi.org/10.1109/TIM.2009.2036347>. Acesso em: 28 set. 2022.

[4] Carvalho T. P., et al. 2019. A systematic literature review of machine learning methods applied to predictive maintenance. Computers & Industrial Engineering. 137: 106024. Disponível em: <https://doi.org/10.1016/j.cie.2019.106024>. Acesso em: 12 out. 2022.

[5] Fávero L. P.; Belfiore, P. 2017. Manual de análise de dados: estatística e modelagem multivariada com Excel®, SPSS® e Stata®. Elsevier, Rio de Janeiro, Brasil.

[6] Confortini, D; Fávero L. P. 2010. Modelos multinível de coeficientes aleatórios e os efeitos firma, setor e tempo no mercado acionário Brasileiro. Pesquisa Operacional. 30(3): 703-727. Disponível em: <https://doi.org/10.1590/S0101-74382010000300011>. Acesso em: 12 out. 2022.

[7] Al-Musthafa M. I. Learning Vector Quantization Based Vibration Analysis for Steam Power Plant Rotating Equipment Fault Diagnosis. In: 2019 International Conference on Technologies and Policies in Electric Power & Energy. IEEE, 2019. p. 1-3. Disponível em: < https://dx.doi.org/10.1109/IEEECONF48524.2019.9102521>. Acesso em: 10 out. 2022.

[8] Soto-Ocampo, C. R.; Mera J. M.; Cano-Moreno J. D.; Bernardo J. L. G. Low-cost, high-frequency, data acquisition system for condition monitoring of rotating machinery through vibration analysis-case study. Sensors, v. 20, n. 12, p. 3493, 2020. Disponível em: <https://dx.doi.org/10.3390/s20123493>. Acesso em: 16 out. 2022

[9] Manwell J. F.; Mcgowan, Jon G.; Rogers, Anthony L. Wind energy explained: theory, design and application. John Wiley & Sons, 2010. Disponível em: <http://doi.org/10.1002/9781119994367>. Acesso em: 16 out. 2022.

[10] R Core Team. R: A language and environment for statistical computing. Viena, Áustria: R Foundation for Statistical Computing, 2022. Disponível em: <https://www.R-project.org/>. Acesso em: 10 set. 2022.

[11] RStudio Team. RStudio: Integrated Development Environment for R. Boston, MA: RStudio, PBC, 2022. Disponível em: <https://www.rstudio.com/>. Acesso em: 10 set. 2022.

Como citar

Silva J. G. M.; Silva J. E. O uso da abordagem multinível para previsão de falhas em aerogeradores. Revista E&S. 2023; 4: e20230110.

Sobre os autores

João Gilberto Máximo Da Silva ,  Alameda João Galego, 988 – Santa Maria; 09560-340 – São Caetano do Sul, São Paulo, Brasil.

José Erasmo Silva , Professor Orientador MBA Data Science e Analytics, Rua Maria Társia, 51 – Jardim Elite; 13417-440. Piracicaba, São Paulo, Brasil.

Link para download: PDF