
29 de novembro de 2024
Aplicação de um modelo de machine learning para prever a evasão escolar
DOI: 10.22167/2675-6528-20240030
E&S 2024, 5: e202400030
Tibério Morais Silva Júnior e José Erasmo Silva
Em um modelo ideal de formação acadêmica, todos os estudantes matriculados em instituições de ensino atingiriam o objetivo de finalizar o curso no prazo estabelecido. Contudo, na realidade, diversas intercorrências surgem no processo educacional, como o abandono e a desistência. Tais fenômenos são frequentemente categorizados por pesquisadores como evasão[1].
Apesar dessa associação, alguns estudiosos sobre o tema, como Tinto[2], afirmam que existe um desalinhamento sobre o que poderia realmente ser definido como evasão, sugerindo que: 1) não há consenso sobre a definição do termo evasão; 2) que essa definição pode, inclusive, ser alterada em função dos contextos individual, institucional ou estatal.
Conforme Silva et al.[1], a evasão escolar apresenta consequências negativas tanto para o estudante quanto para a instituição de ensino. Do ponto de vista do aluno, a evasão não apenas posterga sua formação, mas também resulta em perdas financeiras e de tempo, recursos que poderiam ser direcionados a outras atividades. Para a instituição, a evasão compromete sua eficiência, uma vez que a vaga e os recursos — tanto físicos quanto tecnológicos — previamente alocados para determinado número de alunos passam a ser subutilizados.
Glavam e Cruz[3] ressaltam que a evasão traz transtornos significativos aos educandos, às instituições de ensino e às empresas que buscam mão de obra especializada. Para as instituições educacionais, a evasão impacta diretamente a saúde financeira, pois, ao planejar um curso, os custos associados são projetados com base no número de matrículas.
A evasão resulta em uma diminuição da receita prevista, podendo culminar em déficits financeiros ao término do curso. No contexto empresarial, a evasão amplia a carência de profissionais qualificados, elevando custos e prazos de entrega de produtos. Além disso, a evasão compromete a qualidade de vida dos estudantes, refletindo em empregos precários e salários reduzidos, e reverbera nas famílias, que frequentemente contam com essa renda para fazer frente às suas despesas mensais.
A evasão em cursos de educação profissional é um tema que, apesar da relevância, apresenta uma notável escassez de trabalhos publicados. Essa modalidade de ensino, com suas características peculiares, frequentemente envolve alunos que, paralelamente, estão matriculados em outras instituições de ensino ou possuem compromissos laborais, limitando assim sua dedicação ao curso profissionalizante. Tais particularidades reforçam a importância deste trabalho e a escolha da instituição definida como objeto de estudo, uma entidade que é referência em formação de aprendizes e qualificação profissional. A instituição é privada, mas sem fins lucrativos, e foi fundada em 1947 na Bahia e, posteriormente, em Vitória da Conquista.
Para aprofundar o entendimento sobre as causas da evasão, muitos pesquisadores recorrem a técnicas avançadas de machine learning, que visam identificar as variáveis mais influentes no fenômeno da evasão, possibilitando, assim, a implantação de medidas de prevenção. Por exemplo, Primão[4] e Chung e Lee[5] investigaram, respectivamente, a evasão em diferentes contextos educacionais utilizando técnicas como Árvore de Decisão, Redes Neurais Artificiais e XGBoost. Silva et al.[1] por sua vez, focaram em cursos de graduação à distância no Brasil, empregando o modelo de Regressão Logística Binária.
Dessa forma, a combinação de uma análise aprofundada das características dos cursos profissionalizantes com técnicas avançadas de análise de dados pode oferecer informações importantes sobre a evasão e potenciais estratégias de mitigação.
Dado o contexto, o objetivo deste estudo é aplicar um modelo de machine learning, especificamente a Regressão Logística Binária, para prever a evasão escolar. Dessa forma será possível não só antecipar ações para minimizar a evasão, mas também analisar os fatores associados a ela nos cursos de educação profissional oferecidos pela instituição estudada, em Vitória da Conquista (BA). A amostra empregada neste estudo foi fornecida pela gerência de tecnologia da Informação da instituição. A base de dados fornecida está em formato .xlsx, contendo 2.599 observações e 21 variáveis. Os dados pessoais dos alunos, como CPF, nome, filiação, entre outros, foram omitidos. A base de dados é composta por informações coletadas durante o processo de matrícula nos cursos de educação profissional presenciais oferecidos pela entidade entre 2019 e 2023. As variáveis que compõe essa base de dados estão apresentadas na Tabela 1.
Tabela 1. Variáveis utilizadas no estudo
| Variável | Descrição |
| DataNascimento | Data de nascimento (data) |
| PossuiDeficiência | Indicadora binária de deficiência (categórica) |
| NomeDeficiência | Nome da deficiência, se for o caso (categórica) |
| PosicaoNaFamilia | Posição na família (dependente ou não) |
| QuantidadeDePessoasNoGrupoFamiliar | Quantidade de pessoas na família (numérica) |
| RendaFamiliarBruta | Renda bruta familiar (numérica) |
| RendaPerCapita | Renda per capita (numérica) |
| PossuiVinculoDeTrabalho | Indicadora binária de vínculo empregatício (categórica) |
| PorQueNaoTrabalha | Motivo de não trabalhar (8 categorias) |
| AtividadeEconomica | Atividade econômica na qual trabalha (46 categorias) |
| TipoDeVinculo | Tipo de vínculo (7 categorias) |
| TipoDeInstituicaoDeEnsinoFundamental | Tipo pública ou privada (categórica) |
| TipoDeInstituicaoDeEnsinoMedio | Tipo pública ou privada (categórica) |
| MatriculadoNaEducacaoBasica | Indicadora binária de matrícula (categórica) |
| EgressoNoProgramaDeAprendizagem | Egresso sim ou não (categórica) |
| EgressoNaEducaoBasica | Egresso sim ou não (categórica) |
| EstadoMatrícula | Variável dependente (inicialmente 8 categorias) |
| Cidade | Cidade (34 categorias) |
| Escolaridade | Escolaridade (categórica) |
| NomeTurma | Nome da turma / curso (categórica) |
| PeríodoDaTurmaEmMeses | Tempo em meses do curso (numérica) |
Ao analisar inicialmente a variável “estado matrícula”, identifica-se a presença de oito categorias que descrevem a situação do aluno em relação ao curso. São elas: aprovado, desistente, em processo, evadido, matrícula cancelada, matriculado, reprovado e transferência interna de mesmo título. O status “aprovado” é atribuído ao aluno que frequentou o curso com um percentual de faltas menor ou igual a 25% do total de aulas e foi aprovado nas avaliações de habilidades e competências. “Desistente” e “matrícula cancelada” referem-se aos alunos que se matricularam, mas não compareceram a nenhuma aula. O termo “evadido” é utilizado quando o aluno se matricula, frequenta ao menos uma aula, mas não dá continuidade ao curso. “Reprovado” é o status para aqueles que não obtiveram aprovação nas avaliações ou tiveram um índice de faltas superior a 25% do total de aulas. Os status “matriculado” e “em processo” indicam que o aluno ainda possui matrícula ativa no curso ou já o concluiu, estando em fase de fechamento administrativo. Por fim, “transferência interna de mesmo título” é a categoria para alunos que solicitaram mudança para outra turma do mesmo curso.
Apesar da falta de um consenso na literatura sobre a definição exata do termo evasão, para este trabalho, seguindo orientações da gestão da instituição estudada, considerou-se evadido o aluno que registrou ao menos uma presença durante o curso e, por algum motivo, interrompeu sua frequência. Assim, qualquer aluno com o status “evadido” na variável “estado matrícula” é entendido como evadido. Para analisar a base de dados e estimar a probabilidade de evasão, utilizou-se o Modelo de Regressão Logística Binária, inserido no conjunto de modelos lineares generalizados em que a variável dependente é qualitativa binária, com no máximo duas categorias. Segundo Fávero e Belfiore[6], nesse modelo a variável dependente (evasão) segue uma distribuição de Bernoulli, cuja probabilidade de ocorrência de um evento é , e a probabilidade de ocorrência de um não evento é . Esse objetiva estimar a probabilidade de ocorrência de um evento definido por Y, que se mostra na forma qualitativa dicotômica, sendo que Y = 1 representa a ocorrência do evento, e Y = 0, a ocorrência do não evento. O vetor de varáveis explicativas desse modelo pode ser definido conforme a eq.(1):
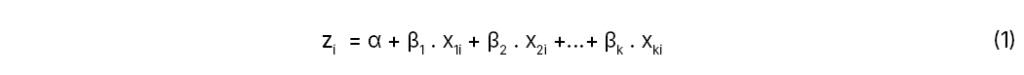
em que Z é denominado logito, α é uma constante, βj (1, 2, …, k) são os parâmetros estimados da variável explicativa Xj (métricas ou variáveis dummy) e o subscrito i representa cada observação da base de dados. No mesmo contexto, o autor descreve que a probabilidade estimada de que um determinado evento ocorra pode ser definida pela eq.(2).
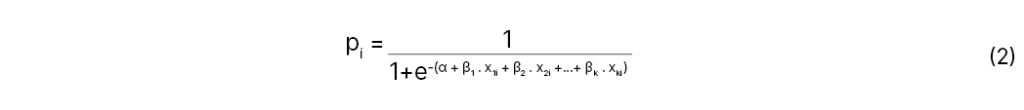
Ao analisar a variável dependente (dicotômica) em um modelo de regressão logística binária, torna-se evidente que a estimativa dos parâmetros da equação de probabilidade não pode ser realizada da mesma forma que nas técnicas convencionais de regressão linear, pois as últimas estimam seus parâmetros pelo método de Mínimos Quadrados Ordinários (MQO). A diferença surge porque, ao estudar a probabilidade de ocorrência de um evento com uma variável resposta qualitativa, o modelo não pode calcular a média ou a variância. Assim, não consegue minimizar a soma dos termos de erro sem uma ponderação arbitrária. Portanto, para estimar os parâmetros de uma equação de probabilidade no modelo de regressão logística, é utilizado o logaritmo da função de verossimilhança (log likelihood function). Para essa função, valores que se aproximam de zero indicam uma maior capacidade de acerto do modelo[6].
Por meio da Tabela 2 é possível observar que a categoria “aprovado” representou uma grande parcela do total de ocorrências.
Tabela 2. Frequência das categorias da variável Estado da Matrícula
| Estado da Matrícula | Observações | Percentual (%) |
| Aprovado | 1450 | 55,79 |
| Matrícula cancelada | 112 | 4,31 |
| Reprovado | 202 | 7,77 |
| Em processo | 397 | 15,28 |
| Matriculado | 92 | 3,54 |
| Desistente | 99 | 3,81 |
| Evadido | 215 | 8,27 |
| Transferência interna mesmo título | 32 | 1,23 |
| Total | 2599 | 100 |
Se somados às outras categorias que representam a ocorrência do não evento (alunos que não evadiram) e comparados com o total de ocorrências do evento (evasão), é possível notar que esses dados se apresentam desbalanceados. Apesar de os dados desbalanceados não serem um problema para a regressão logística binária, é necessário levar isso em consideração na interpretação dos resultados. Analisando o tipo de vínculo profissional, é possível perceber que a maioria dos alunos que preencheram a matrícula não informaram os dados referente a essa variável. Entre os que escolheram alguma categoria, destaca-se a informação “empregado com carteira assinada” (Tabela 3).
Tabela 3. Frequência das categorias da variável “tipo de vínculo”
| Tipo de vínculo | Observações | Percentual (%) |
| Autônomo | 150 | 5,77 |
| Empregado com carteira assinada | 798 | 30,70 |
| Empregado sem carteira assinada | 120 | 4,62 |
| Funcionário público | 32 | 1,23 |
| Não informado | 1404 | 54,02 |
| Outros | 93 | 3,58 |
| Profissional liberal | 2 | 0,08 |
| Total | 2599 | 100 |
Ao analisar o nível de escolaridade dos alunos, entende-se que muitos ainda não haviam concluído o ensino superior, tratando-se de uma amostra formada na maioria por estudantes que haviam concluído ou continuavam cursando o ensino médio (Tabela 4).
Tabela 4. Frequência das categorias da variável “escolaridade”
| Escolaridade | Observações | Percentual (%) |
| Ensino fundamental completo | 92 | 3,54 |
| Ensino fundamental cursando | 66 | 2,54 |
| Ensino fundamental incompleto | 62 | 2,39 |
| Ensino médio completo | 1302 | 50,10 |
| Ensino médio cursando | 617 | 23,74 |
| Ensino médio incompleto | 149 | 5,73 |
| Graduação completo | 97 | 3,73 |
| Graduação cursando | 64 | 2,46 |
| Graduação incompleto | 27 | 1,04 |
| Técnico de nível médio completo | 18 | 0,69 |
| Técnico de nível médio cursando | 43 | 1,65 |
| Técnico de nível médio incompleto | 6 | 0,23 |
| Não preenchido | 56 | 2,15 |
| Total | 2599 | 100 |
Os cursos de aprendizagem profissional, frequentemente referidos como Programa Jovem Aprendiz, predominam em termos de número de matrículas, destacando-se como os principais atrativos para os alunos (Tabela 5). Notavelmente, os cursos de Assistente Administrativo e Design de Sobrancelhas são exceções, sendo os únicos dessa categoria a apresentar um elevado número de matrículas.
Tabela 5. Frequência das categorias da variável NomeTurma
| NomeTurma (curso) | Observações | Percentual (%) |
| Administração de pequenas empresas | 10 | 0,38 |
| Administrador de banco de dados | 19 | 0,73 |
| Alfaiataria feminina | 6 | 0,23 |
| Aprendizagem profissional comercial em serviços Administrativos | 226 | 8,70 |
| Aprendizagem profissional comercial em serviços de supermercados | 63 | 2,42 |
| Aprendizagem profissional de qualificação em serviços administrativos | 595 | 22,89 |
| Aprendizagem profissional de qualificação em serviços de supermercados | 219 | 8,43 |
| Assistente administrativo | 291 | 11,20 |
| Atualização em corte e escova | 11 | 0,42 |
| Atualização profissional para camareira(o) | 1 | 0,04 |
| Auxiliar de cozinha | 16 | 0,62 |
| Bolos artísticos | 48 | 1,85 |
| Cabeleireiro | 8 | 0,31 |
| Coloração, descoloração, reflexos e mechas | 10 | 0,38 |
| Condutor em turismo – cultura, ecoturismo e roteiros | 30 | 1,15 |
| Confeiteiro | 11 | 0,42 |
| Costureiro | 110 | 4,23 |
| Cozinheiro | 3 | 0,12 |
| Cuidador de idoso | 61 | 2,35 |
| Desenvolvimento de lideranças | 21 | 0,81 |
| Design de sobrancelhas | 246 | 9,47 |
| Formação de preço de venda | 16 | 0,62 |
| Gestão financeira para microempresa | 15 | 0,58 |
| Manicure e pedicure | 148 | 5,69 |
| Maquiador | 14 | 0,54 |
| Marketing digital | 47 | 1,81 |
| Modelagem básica para vestuário | 2 | 0,08 |
| Modelagem e confecção de roupas infantis | 6 | 0,23 |
| Preparo de bolos tradicionais | 12 | 0,46 |
| Salgadeiro | 82 | 3,16 |
| Técnicas de arrumação de unidades habitacionais em datas comemorativas | 6 | 0,23 |
| Técnicas de costura e acabamento | 19 | 0,73 |
| Técnicas de depilação | 25 | 0,96 |
| Técnico em computação gráfica | 18 | 0,69 |
| Técnico em estética | 29 | 1,12 |
| Técnico em eventos | 31 | 1,19 |
| Técnico em logística | 31 | 1,19 |
| Técnico em massoterapia | 23 | 0,88 |
| Técnico em podologia | 16 | 0,62 |
| Tendência em penteados | 12 | 0,46 |
| Unhas de fibra | 22 | 0,85 |
| Unhas de gel | 16 | 0,62 |
| Unhas decoradas em 3D | 4 | 0,15 |
| Total | 2599 | 100 |
Em uma análise mais detalhada das origens geográficas dos alunos matriculados nos cursos da instituição estudada, identificou-se a presença de estudantes provenientes de 34 cidades diferentes. A região Sudoeste da Bahia se destacou, especialmente a cidade de Vitória da Conquista que, sozinha, representava 1.417 dessas matrículas.
Tabela 6. Frequência das categorias da variável Cidade
| Cidade | Observações | Percentual (%) |
| Anagé | 5 | 0,19 |
| Aracatu | 108 | 4,1 |
| Barra da Estiva | 14 | 0,54 |
| Barra do Choça | 3 | 0,12 |
| Belo Campo | 66 | 2,54 |
| Brumado | 238 | 9,16 |
| Caatiba | 1 | 0,04 |
| Candiba | 183 | 7,04 |
| Ceraima | 1 | 0,04 |
| Cruz das Almas | 1 | 0,04 |
| Érico Cardoso | 3 | 0,12 |
| Florestal | 1 | 0,04 |
| Gongogi | 24 | 0,92 |
| Guanambi | 210 | 8,08 |
| Ibicoara | 1 | 0,04 |
| Igaporã | 75 | 2,89 |
| Iguá | 6 | 0,23 |
| Ituaçu | 13 | 0,50 |
| Jaicós | 2 | 0,08 |
| Jequié | 198 | 7,62 |
| Macaúbas | 5 | 0,19 |
| Matina | 2 | 0,08 |
| Palmas de Monte Alto | 2 | 0,08 |
| Paramirim | 1 | 0,04 |
| Pilões | 3 | 0,12 |
| Pindaí | 1 | 0,04 |
| Planalto | 2 | 0,08 |
| Pradoso Presidente Jânio Quadros | 7 | 0,27 |
| Salvador | 3 | 0,12 |
| Sebastião Laranjeiras | 1 | 0,04 |
| Tanhaçu | 1 | 0,04 |
| Taperoá | 1 | 0,04 |
| Vitória da Conquista | 1417 | 54,52 |
| Total | 2599 | 100 |
Para representar a ocorrência ou não do evento, foi criada a variável dependente dicotômica “evasão”, contendo o “Y” para representar a existência do evento e o “N” para o não evento (Tabela 7).
Tabela 7. Variável dependente “evasão ‘N’ (não) ou ‘Y’ (sim)”
| N | Y |
| 2384 (91,72%) | 215 (8,27%) |
Após a análise da base de dados, foi verificada a existência de 155 observações sem os dados completos para modelagem e, sendo assim, optou-se por excluí-los, restando 2.444. Além disso, destaca-se que todas as variáveis categóricas foram transformadas em dummy. Segundo Fávero e Belfiore[6], para evitar o erro de ponderação arbitrária com variáveis qualitativas em modelos de regressão logística binária, deve-se utilizar a técnica de variáveis dummy.
O modelo denominado “modelo_evasao” foi desenvolvido para representar a regressão logística implementada utilizando a função glm no RStudio – ambiente de desenvolvimento integrado gratuito para a linguagem de programação R. Nesse modelo, determinou-se “evasão” como a variável resposta, especificando-se também o parâmetro “family” como “binomial”. A Tabela 8 apresenta os resultados desse modelo, destacando os parâmetros estimados (“Estimate”) e a significância estatística das variáveis após o procedimento “stepwise”.
Tabela 8. Resultados do modelo GLM para previsão e análise dos fatores associados à evasão escolar
| Variáveis | Estimate | Std. Error | z-value | Pr(>|z|) | Sig. |
| (Intercept) | -3,0847 | 0,2814 | -10,961 | <0,00002 | *** |
| atividadeeconomica_nao_informado | -0,7009 | 0,2156 | -3,251 | 0,001149 | ** |
| atividadeeconomica_servicos_combinados_de_escrito | 1,2985 | 0,3721 | 3,489 | 0,000484 | *** |
| aprendizagem_profissional_de_qualificacao_em_servicos_administrativos | 1,6137 | 0,2456 | 6,57 | 5,02E-11 | *** |
| aprendizagem_profissional_de_qualificacao_em_servicos_de_supermercados | 1,3105 | 0,3241 | 4,044 | 5,26E-05 | *** |
| assistente_administrativo | 1,2894 | 0,2998 | 4,301 | 1,70E-05 | *** |
| cuidador_de_idoso | 1,7612 | 0,4499 | 3,915 | 9,05E-05 | *** |
| Maquiador | 2,4863 | 0,6818 | 3,646 | 0,000266 | *** |
| tecnico_em_eventos | 2,5269 | 0,475 | 5,32 | 1,04E-07 | *** |
| tecnico_em_logistica | 2,5535 | 0,4745 | 5,381 | 7,41E-08 | *** |
| tecnico_em_massoterapia | 2,2275 | 0,5859 | 3,802 | 0,000144 | *** |
Nota: *** Significante ao nível de 0,001; ** significante ao nível de 0,01, * significante ao nível de 0,05
Após a modelagem estatística utilizando a regressão logística binária, observou-se que as variáveis “atividadeeconomica_nao_informado” e “atividadeeconomica_servicos_combinados_de_escrito” são estatisticamente significantes (Tabela 8). A variável “atividadeeconomica_nao_informado”, com coeficiente negativo, indica uma menor probabilidade de evasão comparada à categoria de referência “atividadeeconomica_atividade_medica_ambulatorial”. Em contraste, a variável “atividadeeconomica_servicos_combinados_de_escrito”, com coeficiente positivo, sugere uma maior probabilidade de evasão entre os alunos que exercem essa atividade econômica.
Além disso, as demais variáveis significantes estão relacionadas ao nome do curso. Por exemplo, a categoria “tecnico_em_logistica” apresenta uma probabilidade 2,5535 vezes maior de evasão comparada ao curso de “administração_de_pequenas_empresas”, que foi utilizado como referência. Isso indica que o tipo de curso escolhido pelo aluno pode ser um fator determinante na sua probabilidade de evadir.
Optou-se por excluir variáveis que não demonstraram significância estatística, seguindo o procedimento de “stepwise”. Essa decisão foi tomada para focar nas variáveis que realmente influenciam a previsão da evasão escolar, alinhando-se ao objetivo preditivo do estudo. No entanto, é relevante mencionar que a inclusão de variáveis não significantes, embora não preditivas, pode proporcionar uma visão mais abrangente das influências potenciais no fenômeno da evasão, dependendo do propósito da análise[6].
Após a análise dos coeficientes é importante analisar as métricas que validam o poder preditivo do modelo. Essa análise foi realizada por meio da curva receiver operating characteristic [ROC], pela curva de sensibilidade e pela curva de especificidade, além da matriz de classificação.
Ao calcular a sensibilidade e a especificidade, é essencial determinar o ponto de corte, ou cutoff, que será usado para classificar as observações com base no cálculo de suas probabilidades. Isso é particularmente relevante quando se introduz uma nova observação na amostra e se deseja prever a probabilidade de essa observação ser classificada como um evento ou não. A classificação ocorre ao comparar o valor estimado da probabilidade pi da nova observação com o valor do cutoff. Se pi for maior do que o cutoff, a observação será categorizada como evento; se pi for menor do que o cutoff, será categorizada como não evento. O cutoff permite avaliar a precisão do modelo com as observações da amostra, assegurando que essa precisão seja mantida ao prever a ocorrência de um evento em novas observações.
A partir da Figura 1 é possível analisar as curvas de sensibilidade e especificidade. Sua análise revela um ponto ótimo de cutoff aproximadamente igual a 0,12, o que representa um equilíbrio entre sensibilidade e especificidade. É notável que a curva de especificidade apresenta uma alta taxa de acertos para quase todos os valores de cutoff, enquanto a curva de sensibilidade exibe um comportamento oposto, com a taxa de acerto diminuindo significativamente para pontos de cutoff superiores a 0,15. Percebe-se ainda que o modelo está bem calibrado para prever o não evento (não evasão). No entanto, sua eficácia na previsão da evasão é menos consistente. Isso sugere que, para valores mais elevados de cutoff, o modelo tende a cometer mais erros ao prever a evasão. Esse comportamento pode impactar negativamente a eficiência geral do modelo. Assim, para aprimorar a capacidade do modelo em prever a evasão, pode ser benéfico considerar a inclusão de novas variáveis explicativas, bem como utilizar uma amostra maior.
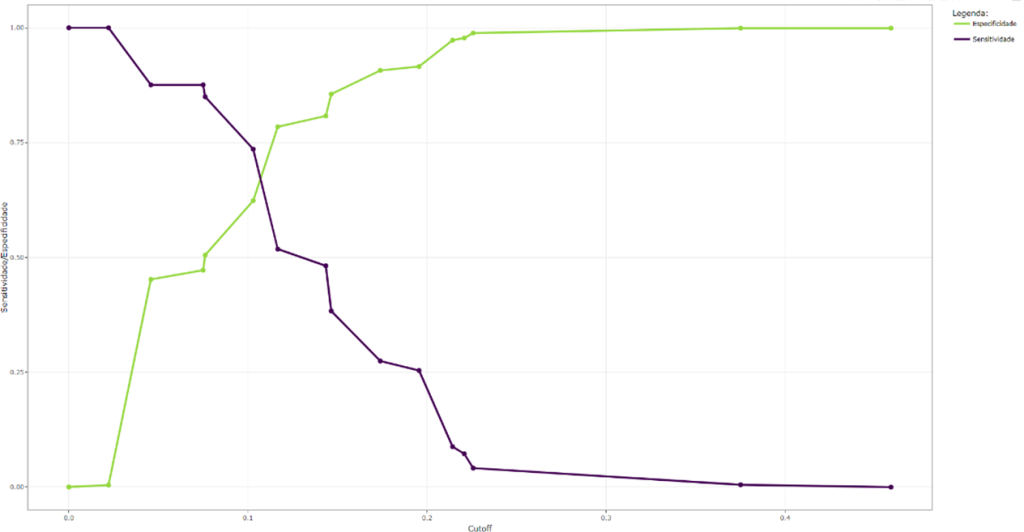
Fonte: Resultados originais da pesquisa.
Para visualizar e obter um maior entendimento a respeito do comportamento preditivo desse modelo, foi gerada uma matriz de classificação para um cutoff igual a 0,10. Mais uma vez, percebe-se a capacidade preditiva desse modelo em relação à previsão do não evento, com 1.404 acertos e apenas 847 erros. No entanto, a matriz confirma a necessidade de ajuste desse modelo quando o objetivo principal de sua utilização for avaliar a ocorrência do evento, a evasão.
Tabela 9. Matriz de Confusão
| Alternativa | Verdadeiro | Falso |
| Verdadeiro | 142 | 847 |
| Falso | 51 | 1.404 |
A sensibilidfade, a especificidade e a acurácia (taxa de acertos global do modelo) podem ser obtidas a partir das informações da matriz de classificação, no RStudio (Tabela 10).
Tabela 10. Estatísticas Matriz de Confusão
| Acurácia | P-valor do teste de Mcnemar | Sensibilidade | Especificidade |
| 0.6326 | < 2 e – 16 | 0.73575 | 0.62372 |
Por fim, a Figura 2 mostra a plotagem da curva ROC. Ela representa o valor da sensibilidade contra 1-especificidade para o modelo utilizado neste trabalho. Observando o valor da área abaixo da curva igual a 0,728, percebe-se que esse modelo se mostrou razoavelmente ao se considerar todos os cutoffs. Dessa forma, para um melhor desempenho desse modelo em relação à capacidade de prever a ocorrência do evento evasão, pode-se sugerir a inclusão de novas variáveis explicativas no modelo e a previsão da evasão utilizando um modelo multinível.
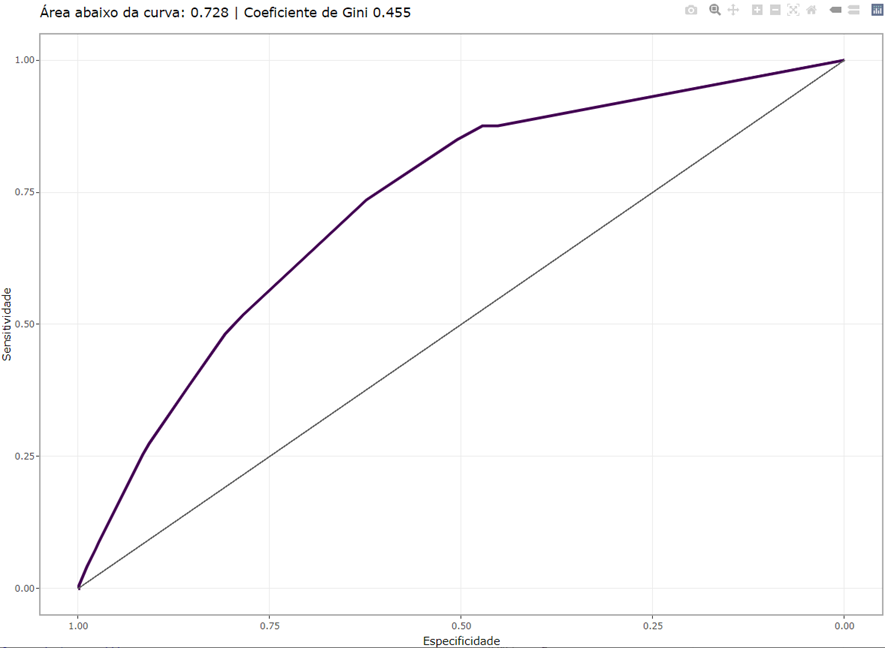
Fonte: Resultados originais da pesquisa.
Este estudo utilizou dados referentes às situações de matrícula dos alunos e suas respectivas características. Empregou-se um modelo de regressão logística binária para avaliar a significância estatística dessas variáveis e a capacidade preditiva do modelo. Observou-se que certas variáveis, tanto relacionadas ao tipo de atividade econômica exercida pelo aluno quanto ao curso em si, possuem uma correlação negativa ou positiva com a evasão. Isso sugere que políticas internas podem ser estrategicamente direcionadas a esses fatores específicos.
Para avaliar a capacidade preditiva do modelo, foram utilizadas métricas como sensibilidade, especificidade, curva de sensibilidade, curva de especificidade e curva ROC. Com um ajuste de cutoff em 0,10, o modelo alcançou acurácia de 0,6326, sensibilidade de 0,73575, especificidade de 0,62372 e área sob a curva ROC de 0,72. O modelo se mostrou eficaz na previsão de não eventos, mas menos preciso na previsão de evasão. Esse comportamento em partes se dá em função do desbalanceamento da base de dados. A diversidade de categorias na variável “EstadoMatrícula” e a ambiguidade de algumas delas trouxeram desafios na análise. Em um cenário com uma organização mais clara dessa variável, é possível que se obtenha um resultado estatístico mais robusto. Além disso, o número limitado de observações pode ter impactado negativamente a avaliação do modelo.
Os resultados apresentados indicam que as atividades econômicas e os tipos de curso são fatores críticos na determinação da evasão escolar. Esse conhecimento permite que os gestores da instituição investigada desenvolvam estratégias direcionadas, como oferecer suporte adicional aos alunos matriculados em cursos com maior risco de evasão, ou criar programas de orientação para estudantes cujas atividades econômicas indicam maior probabilidade de abandono.
Variáveis como data de nascimento, vínculo empregatício, escolaridade, renda familiar, entre outras, que não apresentaram significância estatística no modelo final, podem ser investigadas em estudos futuros utilizando uma amostra maior. Com um conjunto de dados mais robusto, é possível que a influência dessas variáveis na evasão escolar se torne mais evidente, proporcionando insights adicionais sobre os fatores que afetam a decisão dos alunos de continuar ou de abandonar seus cursos.
Este estudo demonstrou que a aplicação de um modelo de regressão logística binária pode não só prever a evasão escolar com razoável precisão, mas também identificar os principais fatores que contribuem para esse fenômeno nos cursos de educação profissional oferecidos pela instituição que foi alvo da pesquisa. Ao antecipar essas tendências, a instituição tem a oportunidade de implementar ações preventivas específicas, potencialmente reduzindo a taxa de evasão e melhorando os resultados educacionais.
Para pesquisas futuras, sugere-se realizar um estudo comparativo entre o modelo de regressão logística binária, o modelo logístico multinomial e o XGBoost, a fim de avaliar qual abordagem oferece melhor desempenho na previsão da evasão escolar.
Referências
[1]Silva, F.C.; Cabral, T.L.O.; Pacheco, A.S.V. 2020. Dropout or permanence? Predictive models for higher education management. Education Policy Analysis Archives 28(149). <https://doi.org/10.14507/epaa.28.5387>.
[2]Tinto, V. 1989. Definir la desercion: Una cuestion de perspectiva. Revista de la Educación Superior. Disponível em: <http://publicaciones.anuies.mx/pdfs/revista/Revista71_S1A3ES.pdf>. Acesso em: 06 jan. 2023.
[3]Glavam, R.B.; Cruz, H.A. 2013. Estudo da Evasão Escolar dos Cursos Profissionalizantes em uma Unidade do Serviço Nacional de Aprendizagem Industrial de Santa Catarina-SENAI. X Simpósio de Excelência em Gestão e Tecnologia. Disponível em:
<https://www.aedb.br/seget/arquivos/artigos13/31818288.pdf>. Acesso em: 06 jan. 2023.
[4]Primão, A.P. 2022. Uso de algoritmos de machine learning para prever a evasão escolar no ensino superior: um estudo no Instituto Federal de Santa Catarina. Dissertação (mestrado profissional) – Universidade Federal de Santa Catarina, Centro Sócio-Econômico, Programa de Pós-Graduação em Administração Universitária, Florianópolis. Disponível em:<https://repositorio.ufsc.br/handle/123456789/238320>. Acesso em: 06 jan. 2023.
[5]Chung, J.Y.; Lee, S. 2019. The Machine Learning-Based Dropout Early Warning System for Improving the Performance of Dropout Prediction. Appl. Sci 9(15) <https://doi.org/10.3390/app9153093>.
[6]Fávero, L.P.; Belfiore, P. 2022. Manual de análise de dados. LTC, Rio de Janeiro, RJ, Brasil.
Como citar
Silva Júnior T.M.; Silva J.E.; Aplicação de um modelo de machine learning para prever a evasão escolar. Revista E&S. 2024; 5: e20240030.
Sobre os autores
Tibério Morais Silva Júnior – Especialista em Data Science e Analytics. Rua Bruno Bacelar, 261, Alto Maron, CEP: 45005-306 – Vitória da Conquista/BA, Brasil
![]() José Erasmo Silva – Professor Orientador MBA Data Science e Analytics – Universidade Federal da Bahia – Programa de Pós-graduação em Contabilidade – PPGCONT– Avenida Reitor Miguel Calmon, s/n Canela – CEP: 40231-300 – Salvador/BA, Brasil
José Erasmo Silva – Professor Orientador MBA Data Science e Analytics – Universidade Federal da Bahia – Programa de Pós-graduação em Contabilidade – PPGCONT– Avenida Reitor Miguel Calmon, s/n Canela – CEP: 40231-300 – Salvador/BA, Brasil
Quem editou este artigo
Luiz Eduardo Giovanelli





































