Inteligência Artificial
Modelagem
Phyton
Séries Temporais
09 de agosto de 2024
Melhores práticas e erros comuns na modelagem de séries temporais
DOI: 10.22167/2675-6528-20240028
E&S 2024, 5: e20240028
José Erasmo Silva
Uma série temporal é um conjunto de dados ordenados cronologicamente. Alguns exemplos são níveis diários de poluição em São Paulo, temperaturas mensais em Cananeia, índices diários de Bolsas de Valores, chuva anual em Fortaleza, média anual de manchas solares, marés no porto de Santos, entre outros[1].
A previsão de séries temporais é um campo em crescimento e importante em áreas que vão da economia à engenharia. No entanto, a aplicação de técnicas preditivas enfrenta frequentemente desafios decorrentes de metodologias inadequadas, que podem levar a resultados enganosos. Este artigo revisou críticas comuns na literatura científica, como as discutidas por Hewamalage et al.[2] e Zemkoho[3], que destacaram os erros frequentes na avaliação de modelos de séries temporais e as implicações práticas de tais erros nos campos de pesquisa e gestão.
Um erro comum na implementação da previsão de séries temporais é a seleção inadequada de métricas de avaliação, o que não apenas distorce a visão da eficácia do modelo, mas também leva a decisões abaixo do ideal. Por exemplo, Hewamalage et al.[2] criticam o uso excessivo do erro quadrático médio (MSE) e do erro médio absoluto (MAE) sem levar em conta características específicas dos dados, como sazonalidade e não estacionariedade. A Figura 1 ilustra isso, mostrando que as previsões baseadas na média dos dados de treinamento podem ser inadequadas. Observa-se que a previsão (linha tracejada) é uma linha horizontal constante que reflete a média dos dados de treinamento. Esta abordagem ignora completamente as tendências e a sazonalidade presentes nos dados. Usar métricas como MSE e MAE sem considerar essas características pode levar a avaliações enganosas. Embora estes indicadores possam ser adequados em alguns casos, não conseguem captar a dinâmica complexa das séries temporais, tais como tendências e sazonalidade. Métricas de avaliação mal escolhidas podem resultar em previsões que parecem satisfatórias em termos de erro médio, mas que na verdade não conseguem refletir a realidade subjacente dos dados temporais.
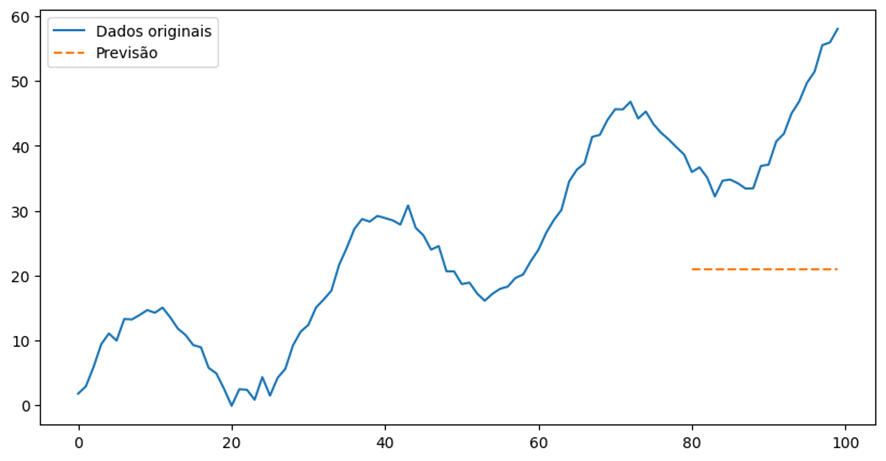
Fonte: Resultados originais da pesquisa.
Nota: MSE: 490,0026905230682, MAE: 20,511124321687145.
Outro erro comum destacado na literatura envolve o tratamento inadequado da dependência do tempo em modelos preditivos. Muitos analistas não consideram que as observações numa série temporal estão correlacionadas, o que contradiz os pressupostos básicos de muitos métodos estatísticos tradicionais. Como explicou Zemkoho[3], ignorar a autocorrelação entre períodos consecutivos pode levar à subestimação da incerteza e a previsões que não refletem a verdadeira dinâmica dos dados. Esta supervisão é particularmente importante em modelos como o autorregressivo integrado de médias móveis (ARIMA) e a suavização exponencial, nos quais a suposição de independência pode invalidar as previsões e comprometer a integridade das conclusões obtidas. A Figura 2 mostra que as previsões geradas pelo modelo de suavização exponencial (linha tracejada) não conseguem capturar as tendências e a sazonalidade presentes nos dados originais. A previsão tenta capturar uma média móvel dos dados, mas não segue a verdadeira dinâmica da série temporal. Isto resulta em previsões que não refletem totalmente as flutuações e a dinâmica dos dados reais.
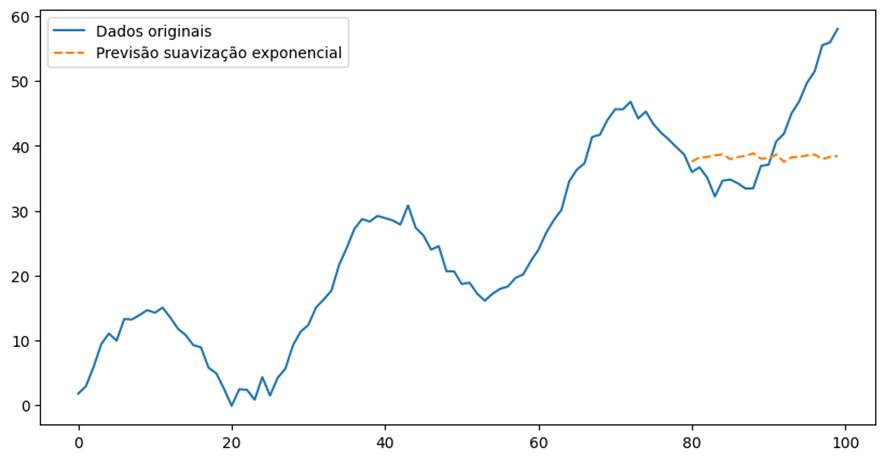
Fonte: Resultados originais da pesquisa.
Com base na discussão sobre a importância de considerar a dependência do tempo ao modelar séries temporais, é igualmente importante abordar outro conceito fundamental na análise de séries temporais: a estacionariedade. Como enfatizou Zemkoho[3], a suposição de que uma série temporal é estacionária — ou seja, que suas propriedades estatísticas, como média e variância, não mudam ao longo do tempo — é crucial para a aplicação de muitos modelos estatísticos. Contudo, muitas séries reais apresentam tendências ou sazonalidade, o que viola esta suposição. A falha em testar e ajustar a não estacionariedade pode resultar num modelo que parece adequado, mas que na verdade não consegue captar a dinâmica subjacente dos dados, resultando em previsões imprecisas e potencialmente dispendiosas.
Uma vez identificada a não estacionariedade por meio dos testes apropriados, técnicas como transformações diferenciais e logarítmicas são frequentemente usadas para estabilizar a variância e tornar a média constante ao longo do tempo, ou seja, essas técnicas são usadas para preparar dados para modelos que assumem estacionariedade, como modelos ARIMA. Porém, a escolha do grau de diferenciação ou tipo de transformação deve ser cuidadosamente ajustada para evitar a superdiferenciação, que pode introduzir ruído e causar a perda de informações importantes do sinal original. Portanto, recomenda-se determinar o número apropriado de diferenças para garantir a adequação do modelo sem comprometer a integridade dos dados por meio da validação cruzada e do uso de critérios de informação, como o critério de informação de Akaike (AIC).
A implementação de técnicas de transformação diferencial e logarítmica é crucial para lidar com a não estacionariedade de séries temporais e pode ser alcançada usando bibliotecas como pandas e statsmodels que rodam em Python. Por exemplo, a função adfuller() no módulo statsmodels.tsa.stattools permite executar testes Dickey-Fuller aumentados (ADF) diretamente em seus dados enquanto usa as bibliotecas numpy ou pandas para simplificar transformações como transformações logarítmicas por meio de operações vetoriais. Resumindo, essas ferramentas não apenas facilitam o trabalho, mas também ajudam a melhorar a qualidade da análise de séries temporais.
Interpretar os resultados dos testes de estacionariedade e aplicar as transformações corretas são desafios que exigem um profundo conhecimento do background técnico e dos dados. Mesmo ao utilizar ferramentas avançadas, a exemplo da linguagem Python, é preciso estar atento a possíveis armadilhas, como interpretação incorreta de p-valores ou aplicação desnecessária de diferenciação, que podem comprometer a qualidade das previsões. Para mitigar estes riscos, recomenda-se uma abordagem de modelação iterativa, em que cada passo é validado utilizando a visualização de dados e o ajuste fino de métricas de desempenho, como por exemplo o AIC. Isso garante que as mudanças realmente melhorem o poder preditivo do modelo sem introduzir vieses ou ajustes excessivos.
O gráfico da Figura 3 mostra os dados originais de uma série temporal (linha azul) com tendências e sazonalidade, comparados com os dados diferenciados (linha laranja) e transformados logaritmicamente (linha verde). Os resultados do teste ADF nos dados originais indicaram que a série não era estacionária (estatística ADF de 0,292 e p-valor de 0,977). Após a diferenciação, a série tornou-se estacionária (estatística ADF de -6,094 e p-valor de 1,02e-07). Transformar a série para estacionariedade é um passo necessário para muitas técnicas de modelagem de séries temporais. No entanto, essas transformações devem ser realizadas cuidadosamente para garantir que os dados estejam adequadamente preparados para a modelagem subsequente.
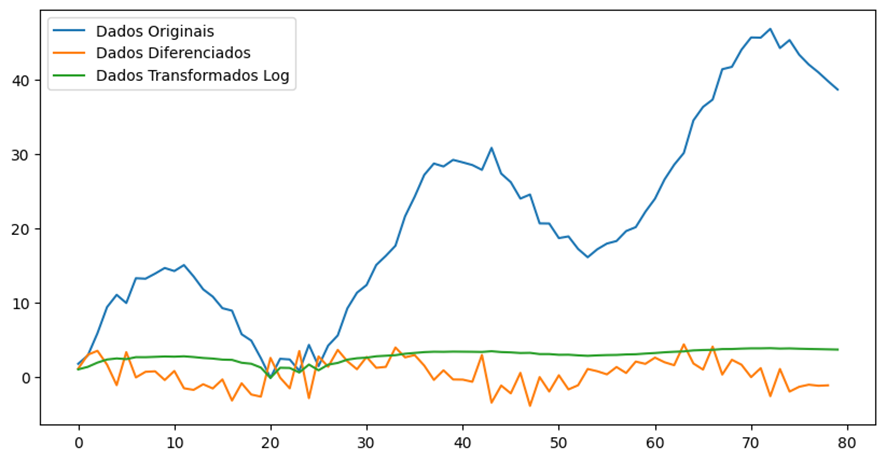
Fonte: Resultados originais da pesquisa.
Nota: Estatística ADF: 0,29240217494006726; p-valor: 0,976993204902754; estatística ADF após a diferenciação: -6,093854884454573; p-valor após a diferenciação: 1,0211713068650123e-07.
Hewamalage et al.[2] enfatizam que, embora estes testes sejam úteis, também é importante compreender suas limitações e interpretar corretamente os seus resultados. Por exemplo, eles alertam contra a dependência excessiva de resultados de testes automatizados de estacionariedade, que podem não conseguir captar nuances importantes na estrutura temporal dos dados. Por outras palavras, embora estes testes possam fornecer uma indicação útil de estacionariedade, eles não substituem uma compreensão profunda e uma análise cuidadosa dos dados.
Vale a pena notar que a implementação eficaz de modelos de séries temporais em cenários do mundo real requer mais do que um ajuste preciso; requer também uma compreensão clara do contexto em que as previsões são aplicadas. Em setores como o financeiro, o varejo e a energia, modelos robustos podem significar a diferença entre lucros e perdas significativas. Portanto, além da precisão, os modelos também devem ser adaptáveis e sensíveis às mudanças econômicas, sazonais e regulatórias. Recomenda-se a colaboração contínua entre analistas de dados e especialistas no domínio para garantir que as previsões não sejam apenas precisas, mas também relevantes e aplicáveis às decisões estratégicas que enfrentam.
O desenvolvimento de técnicas de modelagem de séries temporais levou a avanços significativos, especialmente à integração de métodos de aprendizado de máquina. Abordagens híbridas que combinam técnicas estatísticas tradicionais com métodos de aprendizado de máquina provaram ser particularmente eficazes. Por exemplo, os modelos ARIMA podem ser usados para capturar padrões lineares em dados, enquanto as redes neurais são usadas para modelar componentes não lineares. Esta combinação pode melhorar significativamente os resultados de previsão em comparação com o uso de um único método[4].
Recentemente, a eficácia dos modelos híbridos foi demonstrada na competição M4 de previsão de séries temporais, organizada por Spyros Makridakis e pelo International Institute of Forecasters (IIF). A competição M4, parte de uma série de competições iniciadas em 1982 por Makridakis, envolveu a previsão de 100.000 séries temporais usando 61 métodos diferentes, destacando a importância dessa abordagem [5],[6]. Atualmente, a M4 foi sucedida pela M5, continuando a tradição de avaliar e melhorar métodos de previsão. No entanto, é importante destacar que a precisão dessas previsões depende da escolha adequada das métricas de avaliação e da implementação correta das técnicas de validação, como a validação cruzada, por exemplo[7].
Além disso, a combinação de diferentes arquiteturas de redes — como recurrent neural networks (RNN), long short-term memory (LSTM) e convolutional neural networks (CNN) — tem mostrado desempenho interessante em várias aplicações ao capturar padrões complexos e não lineares presentes nos dados[2].
O avanço contínuo das tecnologias emergentes, como aprendizado de máquina e inteligência artificial, promete não apenas aumentar a precisão das previsões, mas também automatizar e otimizar processos de análise de dados em escala. No futuro, espera-se que modelos preditivos se tornem ainda mais integrados com sistemas de tomada de decisão em tempo real, fornecendo percepções instantâneas e democratizando o acesso à análise de dados.
Referências
[1] Morettin P.A.; Toloi C.M.C. Análise de séries temporais: Modelos lineares univariados. 3ed. São Paulo: Blucher; 2018.
[2] Hewamalage H.; Ackermann K.; Bergmeir C. Forecast evaluation for data scientists: common pitfalls and best practices. Data Mining and Knowledge Discovery. 2023; 37(2): 788-832. https://doi.org/10.1007/s10618-022-00894-5.
[3] Zemkoho A. A basic time series forecasting course with Python. Operations Research Forum. 2023; 4(2): 1-43. https://doi.org/10.1007/s43069-022-00179-z.
[4] Zhang G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing. 2003; 50: 159-175. https://doi.org/https://doi.org/10.1016/S0925-2312(01)00702-0.
[5] Smyl S. A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. International Journal of Forecasting. 2020; 36(1): 75-85. https://doi.org/10.1016/j.ijforecast.2019.03.017.
[6] Makridakis S.; Spiliotis E.; Assimakopoulos V. The M4 Competition: 100,000 time series and 61 forecasting methods. International Journal of Forecasting. 2020; 36(1): 54-74. https://doi.org/10.1016/j.ijforecast.2019.04.014.
[7] Bergmeir C.; Benítez J.M. On the use of cross-validation for time series predictor evaluation. Information Sciences. 2012; 191: 192-213. https://doi.org/10.1016/j.ins.2011.12.028.
Como citar:
Silva J.E. Melhores práticas e erros comuns na modelagem de séries temporais. Revista E&S. 2024; 5: e20240028.
Sobre o autor
José Erasmo Silva ![]() – Professor Orientador MBA Data Science e Analytics – Universidade Federal da Bahia – Programa de Pós-graduação em Contabilidade – PPGCONT– Avenida Reitor Miguel Calmon, s/n Canela – CEP: 40231-300 – Salvador/BA, Brasil
– Professor Orientador MBA Data Science e Analytics – Universidade Federal da Bahia – Programa de Pós-graduação em Contabilidade – PPGCONT– Avenida Reitor Miguel Calmon, s/n Canela – CEP: 40231-300 – Salvador/BA, Brasil
Quem editou este artigo
Luiz Eduardo Giovanelli